傅里叶变换

用傅里叶级数或变换表示的函数可由逆过程完全重建（复原），而不丢失信息。这它允许我们工作在傅里叶域，然后返回到函数的原始域中，而不会丢失任何信息。

---

频域：从频域角度看这个世界，世界或许是静止的

分解图示，对于每一个频率，都还有一个相位大小。因此对时域进行分解，可以获得相位、频率和振动大小。

---

傅里叶级数

三角函数系（集合）

$$\sin nx, \cos nx, n = 0, 1, 2, ……$$

正交概念

$$\int^{\pi}_{-\pi} \sin nx \cdot \cos mx \mathrm{dx} = 0$$

$$\int^{\pi}_{-\pi} \cos nx \cdot \cos mx \mathrm{dx} = 0 \space( n\neq m)$$

$$\int^{\pi}_{-\pi} \sin nx \cdot \sin mx \mathrm{dx} = 0 \space( n\neq m)$$

使用积化和差可以证明.

特殊的，有

$$\int^{\pi}_{-\pi} \sin nx \cdot \sin nx \mathrm{dx} = \pi$$

傅里叶级数

当$f(t)$周期为$2\pi$时，有

$$f(t) = \sum^{\infty}_{n=0}a_n\cos nx + \sum^{\infty}_{n=0}b_n\sin nx$$

其中

$$a_n = \frac{1}{\pi} \int^{\pi}_{-\pi}f(x)\cos nx \mathrm {dx}$$

$$b_n = \frac{1}{\pi} \int^{\pi}_{-\pi}f(x)\sin nx \mathrm {dx}$$

对于一个周期函数$f(t) = f(t + 2L)$，可以展开为：

$$f(t) = \frac{a_0}{2} + \sum^{\infty}_{n=1}{a_n \cdot \sin(n\omega t + \phi_n)}$$

傅里叶变换

欧拉公式

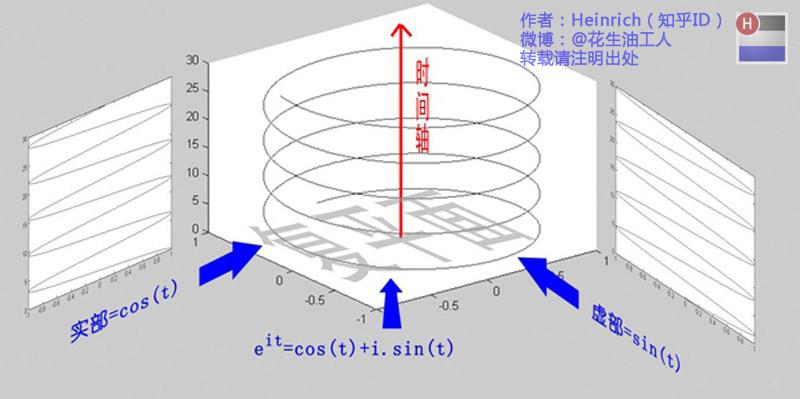
根据欧拉公式，如果将$x$变为$\pi t$，则代表给定时间，正交基的一种组合。可以视为平面上的转动，同样如果是逆时针转动，则取负号。

$$e^{ix} = \cos x + i\sin x$$

当$x=\pi$时，原式变为

$$e^{i\pi} + 1 = 0$$

又有

$$\cos \theta = \frac{1}{2}(e^{i\theta} + e^{-i\theta})$$

$$\sin \theta = \frac{1}{2i}(e^{i\theta} - e^{-i\theta})$$

将其带入傅里叶级数的一般形式

$$f(t) = f(t + T) = \frac{a_0}{2} + \sum^{\infty}_{n=1}{(a_n \cos n\omega t + b_n \sin n\omega t)}$$

可推出

$$f(t) = \sum^{\infty}_{-\infty}C_ne^{in\omega t}$$

其中系数

$$C_n = \frac{1}{T}\int^{T}_{0}f(t)e^{-in\omega t}\mathrm{dt}$$

变换

需要满足下列条件，才可以进行变换

1. 具有有限个间断点
2. 具有有限个极值点
3. 绝对可积

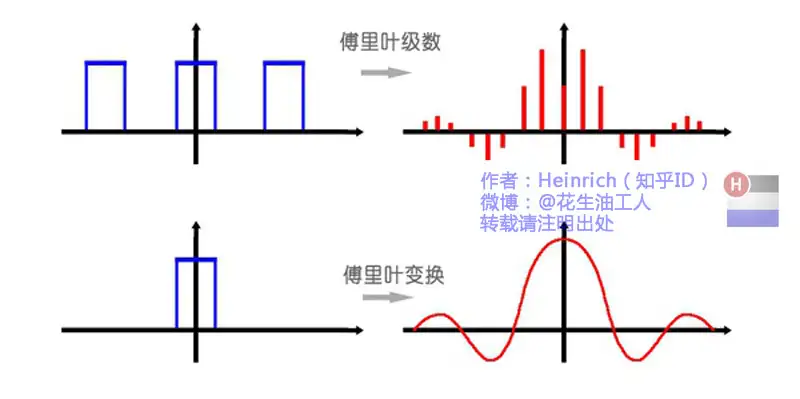
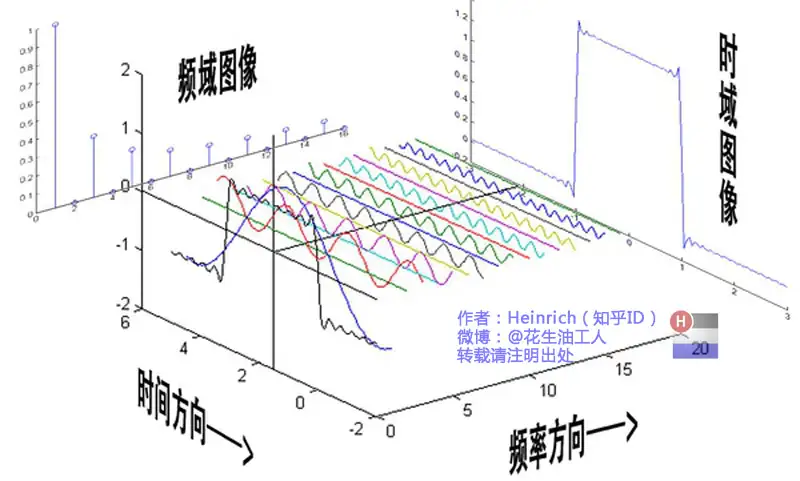
面对有周期函数，我们可以将时域上的图像转换到频域，如上图所示，其中$\Delta\omega$称为基频率。
面对无周期函数，我们可以认为周期为无穷大，那么此时$\Delta\omega = 2\pi/T$就会变得无穷小，那么在频域上就会形成连续的曲线，即

$$T\rightarrow\infin$$

$$\int^{\frac{T}{2}}_{-\frac{T}{2}}dt\rightarrow\int^{\infin}_{-\infin}dt$$

$$n\omega_0\rightarrow\omega$$

$$\sum^{\infin}_{-\infin}\Delta\omega = \int^{\infin}_{-\infin}d\omega$$

那么在有周期的情况下进行替换，可得

$$f(t)=\frac{1}{2\pi}\int^{\infin}_{-\infin}\int^{\infin}_{-\infin}f(t)e^{-i\omega t}dt\space e^{i\omega t}d\omega$$

那么傅里叶变换即为

$$F(\omega) = \int^{\infin}_{-\infin}f(t)e^{-i\omega t}dt$$

逆变换为

$$f(t) = \frac{1}{2\pi}\int^{\infin}_{-\infin}F(\omega)e^{i\omega t}d\omega$$

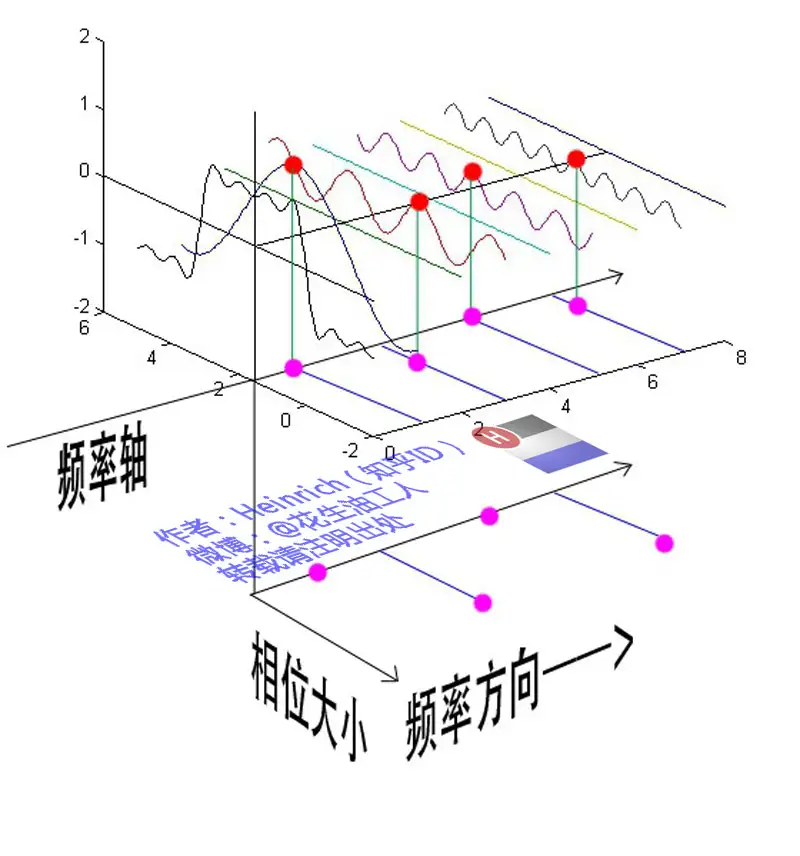
对于频域，我们可以改写为复数形式

$$F(\omega) = R(\omega) + iI(\omega)$$

或者写为指数形式

$$F(\omega) =|F(\omega)|e^{i\phi(\omega)}$$

其中，$|F(\omega)|$称为幅度谱，$\phi(\omega)$称为相位谱。

$$|F(\omega)| = \sqrt{R^2(\omega) + I^2(\omega)}$$

$$\phi(\omega) = arctg\frac{I(\omega)}{R(\omega)}$$