图论

图

简单图

简单图是一种不存在自环或重边的无向图。即任意两个顶点之间最多只有一条边，并且没有顶点连接到其自身。

度数

顶点的度数是指连接到该顶点的边的数目。在无向图中，度数表示为顶点连接的边数。在有向图中，度数分为入度（指向该顶点的边数）和出度（从该顶点出发的边数）。

悬挂点

悬挂点是度数为1的顶点。也就是说，只有一条边连接到该顶点。

奇度点、偶度点

• 奇度点：度数为奇数的顶点。
• 偶度点：度数为偶数的顶点。

握手定理

握手定理指出，在任意一个无向图中，所有顶点的度数之和等于边数的两倍。即：

$$\sum_{v \in V} \deg(v) = 2|E|$$

其中 $\deg(v)$ 表示顶点 $v$ 的度数，$|E|$ 表示边的数目。

正则图

正则图是一种特殊的图，其中所有顶点的度数都相同。如果图中的每个顶点的度数都是 $k$，那么这个图被称为 $k$-正则图。

完全图

完全图是一个简单图，其中任意两个不同的顶点之间都有一条边。包含 $n$ 个顶点的完全图通常表示为 $K_n$。

二部图（二分图）

二部图是一种图，其中顶点集可以分为两个不相交的子集 $U$ 和 $V$，使得图中的每条边都连接一个 $U$ 中的顶点和一个 $V$ 中的顶点。换句话说，二部图中没有顶点之间的边。

完全二部图

完全二部图是二部图的一种特殊情况，其中 $U$ 集中的每个顶点都与 $V$ 集中的每个顶点相连。包含 $|U| = m$ 和 $|V| = n$ 的完全二部图通常表示为 $K_{m,n}$。

入度、出度、度数：

图的同构

两个图 $G_1 = (V_1, E_1)$ 和 $G_2 = (V_2, E_2)$ 被称为同构的，如果存在一个双射映射 $f: V_1 \to V_2$，使得对于任意的顶点 $u, v \in V_1$，当且仅当 $(u, v) \in E_1$ 时，有 $(f(u), f(v)) \in E_2$。

补图、自补图

• 补图：给定一个图 $G = (V, E)$，它的补图 $\overline{G}$ 是一个图，满足 $\overline{G}$ 的顶点集与 $G$ 相同，并且 $\overline{G}$ 中的边集是 $G$ 中不存在的边的集合。
• 自补图：一个图 $G$ 如果与它的补图 $\overline{G}$ 同构，则称 $G$ 是自补图。

子图

子图是一个图的部分顶点及其关联的边形成的图。

• 支撑子图：包含原图的所有顶点的子图。

支配集

(1)V1、V2、V3不是支配集——>都不与V5相邻

(2)V5、V6、V7构成支配集——>与剩余点都相邻，但不是极小支配集，因为移去V5仍是支配集

(3)V1、V3、V5是极小支配集但不是最小支配集——>由(2)知最小支配集可只包含两个顶点

(4)V6、V3既是极小支配集又是最小支配集

(5)V6、V7也是最小支配集

性质

1、对于V中任意一个顶点而言，它或者属于支配集，或者与支配集中的一个元素相邻

2、一个图中极小支配集可能不唯一

3、一个图中最小支配集可能不唯一

4、最小支配集一定是极小支配集，但极小支配集不一定是最小支配集

5、特殊图中的支配集

(a)在任意简单图G=(V,E),V都是支配集

(b)完全图Kn(n≥3)的支配数为1

©完全二分图Kn,m 的支配数为min(n,m)

点独立集

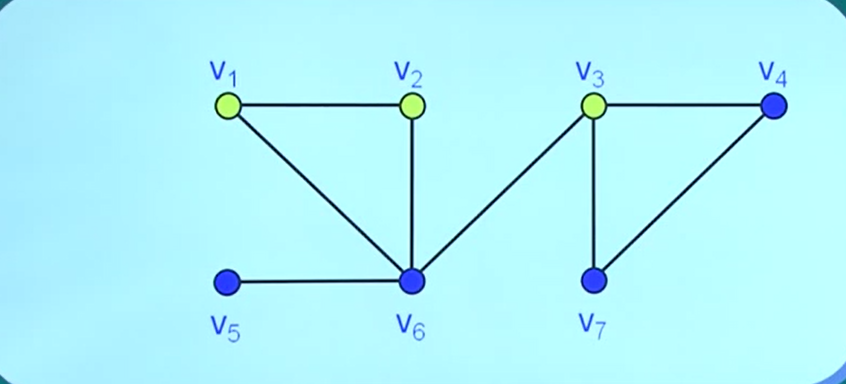
(1)V1、V2、V3不是独立集——>V1、V2相邻

(2)V1、V3是独立集但不是极大独立集——>还可以向其中添加顶点V5

(3)V4、V6是极大独立集但不是最大独立集——>由(2)知顶点数可为3

(4)V1、V3、V5既是极大独立集也是最大独立集

性质

1、极大独立集不是任何其它独立集的子集

2、若S是G的极大独立集，则对任意u∈V-S，都存在v∈S，使得u,vv相邻

3、一个图的极大独立集可能不唯一

4、一个图的最大独立集可能不唯一

5、最大独立集一定是极大独立集，极大独立集不一定是最大独立集

6、特殊图中的独立集

(a)在任意图中，空集都是独立集

(b)完全图Kn(n≥3)的独立数为1

©完全二分图Kn,m 的独立数为max(n,m)

独立数和支配数之间的关系

定理1：一个独立集也是支配集当且仅当它是极大独立集。

定理2：简单无向图的极大独立集也是极小支配集（对偶关系，注意是极大极小，不是最大最小）

点覆盖

(1)V1、V2、V3不是点覆盖——>V5,V6这条边的两个顶点都未被包括

(2)V1、V2、V6、V4、V6、V7是点覆盖但不是极小点覆盖——>可将V2移去

(3)V1、V2、V3、V5、V7是极小点覆盖但不是最小点覆盖

(4)V1、V3、V4、V6既是极小点覆盖也是最小点覆盖

性质

1、在极小点覆盖中，不存在所有相邻顶点都在V*中的顶点

2、一个图的极小点覆盖可能不唯一

3、一个图的最小点覆盖可能不唯一

4、最大点覆盖一定是极小点覆盖，极小点覆盖不一定是最小点覆盖

5、明显有β(G)≥γ(G)

6、特殊图中的点覆盖

支配、独立与覆盖

支配：能够与所有点相连

独立：点集内的点不相连

覆盖：能够与所有边建立联系